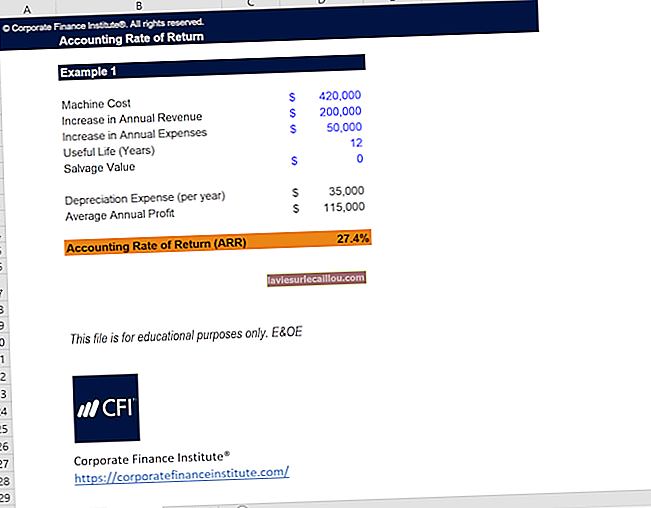
Koncept časovne vrednosti denarja navaja, da je denar, prejet danes, bolj dragocen kot denar, prejet kasneje. Razlog je v tem, da se nekdo, ki se strinja, da bo pozneje prejel plačilo, odreče možnosti, da ta denar vloži takoj. Poleg tega inflacija sčasoma postopoma zmanjšuje kupno moč denarja, zaradi česar je zdaj bolj dragocen. Edini način, da nekdo pristane na zamudo pri plačilu, je, da mu plača privilegij, ki je znan kot dohodek od obresti.
Na primer, če ima oseba zdaj 10.000 ameriških dolarjev in jo investira po 10-odstotni obrestni meri, bo z enoletnim porabljanjem denarja zaslužila 1000 dolarjev. Če namesto tega eno leto ne bi imela dostopa do te gotovine, bi izgubila 1000 dolarjev obresti. Prihodki od obresti v tem primeru predstavljajo časovno vrednost denarja. Če razširimo primer, kakšno je trenutno izplačilo gotovine, pri katerem bi bila oseba brezbrižna, da bi prejela gotovino zdaj ali v enem letu? Kolikšen je v bistvu znesek, ki bo ob 10% naložbi v enem letu enak 10.000 USD? Splošna formula, uporabljena za odgovor na to vprašanje, znana kot sedanja vrednost 1, ki zapade v N obdobjih, je: